記錄學習內容。看網路上大大們的文章和影片,做些紀錄。
還不太了解,內容可能有錯誤。
教學來源(這3篇教學一起看,以下筆記和截圖來自這3篇教學):
用動態規劃解決問題:零壹背包問題(0/1 Knapsack Problem)
4.5.1 0/1 Knapsack Problem (Program) - Dynamic Programming
筆記
背包問題,背包只能裝 重量 max_weight = 1000公克
現在有4個東西 :
A 1200元 , 200公克
B 1500元 , 500公克
C 1500 元 ,300公克
D 4000元 , 850公克
要在小於 背包裝的重量(1000公克之內) , 裝最大價值($$$$)
一開始想法會是 ,看每個東西的 1公克 值多少錢 ,然後錢錢 由大排到小 。
所以:
A 6元 , 1公克
B 3元 , 1公克
C 5 元 ,1公克
D 4.7元 , 1公克
先選A 在選 C ,在選 D ,在選B
200公克 + 300公克 + 850公克 + 500公克
但是 這邊是 0/1 Knapsack Problem 問題 ,0/1就是物品只能選或不選 。
所以 這樣 會不好判斷 ,如果選了 A、C 、D
200+ 300 +850 = 1350 > 背包重量1000
DAA - 0-1 Knapsack(截圖來自這篇教學)
如果背包重量60kg,給了ABC三樣東西 , 要在不超過背包重量的情況下 ,放東西到$$$最多。
如圖 , 價值 依序是 10 > 7 >6 , 所以 先選A ,在選B,在選C 。
選了A ,選了B 之後的價值會變成 100+280 =380$$$ 。重量會是10 +40=50
,所以就不能在選C了。所以最大$$$就會是380$$$
這樣就可以看出0/1問題 不能用Greedy approach了。
因為選B和C 價值更高!!!
B+C 的 價值 為 280+ 120 = 400 >380!!!
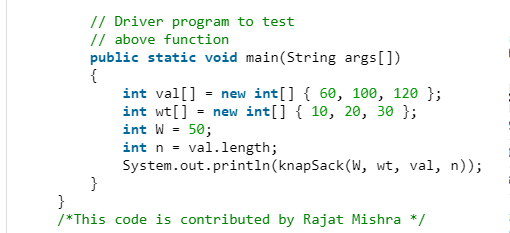
代表每個物品的價值:
int val[] = new int[] { 60, 100, 120 };
代表每個物品的重量:
int wt[] = new int[] { 10, 20, 30 };
背包重量:
int W = 50

如果 物品的重量 大於 背包重量 。跳過 。 到剩餘物品的背包問題(遞迴繼續)。
如果物品的重量 小於 背包重量 。
會有兩種情況 :
1 選擇這個物品到背包 : 所以 總價值會變成-- >這個物品的價值 + 剩餘物品的 背包問題(遞迴繼續) 。 然後總重量記的要扣掉該物品的重量。
2 不選擇這個物品 -- >剩餘物品的 背包問題(遞迴繼續)
這種 選 或 不選 的問題 通常長這樣 :
往左邊 是 不選這個物品 , 往右邊 是 選這個物品 。
然後這種問題的時間複雜度通常是O(2^n) ,簡單的記法 就是
1個func 生成 2個func 。
然後通常這種問題 ,都會重複計算 ,所以可以用動態規劃的方法。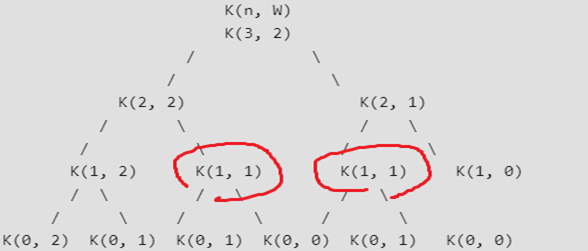
選 或 不選 的問題 ,跟數學有關:
高一下數學2-3A觀念04係數性質的內涵
https://www.youtube.com/watch?v=ZJ1_bf3lheg&list=PLZruNYXiv2mB2VTi8erx5p9p1Z5mQHkR6&index=127&ab_channel=%E5%91%82%E5%86%A0%E7%B7%AF
用了一個二維陣列 int [物品個數][ 總重量]
這邊有舉例 int [物品個數][ 總重量]
物品個數 就是 縱坐標 0 1 2 3 , 橫坐標是 重量 1 到 總重量 。
這邊只寫到6 ,先把它想成50kg這樣,應該比較好理解:
這邊 會變成 button –up ,一般迴圈的方法。
所以程式寫法 會是
int K[][] = new int[物品個數][ 背包總重量50kg];
For 0…物品個數 (i)
For 0…背包總重量50kg (w)
IF ( 物品重量 (10) <= w (10) )
k[物品][w] = MAX (val[物品] + K[物品- 1][w - wt[物品]] , K[物品-1][w] )
else //如果物品重量 大於 現在重量 ,就不能放 ,所以價值維持上一個物品的
K[i][w] = K[i - 1][w];
這邊的時間複雜度,就會是 物品個數 * 背包總重量
空間複雜度 ,就是二維陣列的size -- >物品個數 * 背包總重量
這個方法是 迴圈 和 陣列 。
或者也可以用recursion + memoization = DP(遞迴 和 陣列的方式)。教學文章裡有教,跳過。
這個看不太懂 :
每個K[][]的意思應該是 : 這個物品在這個重量下(放或不放)的最大價值
教學參考(截圖來自這部教學影片):
4.5.1 0/1 Knapsack Problem (Program) - Dynamic Programming
結果會類似這樣: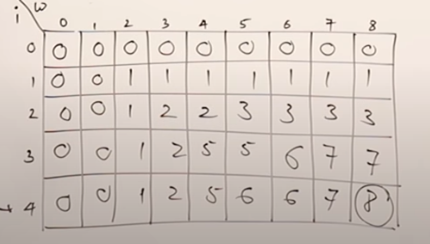
那要怎麼知道最後選了哪些物品 ?
如果第ith 和[ith + 1] 物品 ,重量一樣,但是價值不一樣。代表ith 或[ith + 1] 某個物品有放到袋子裡 。
如果兩個東西價值不等於 ,代表有一個東西會放到袋子裡(看程式寫法,有些是i,有些是i+1)
如圖,大大的程式: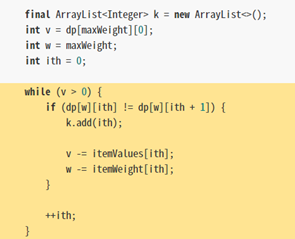
如圖:
8跟7 價值不同,所以代表有放4這個東西 ,扣掉4這個東西的重量和價值。
之後跑到3這個東西 ,繼續跟上一個物品比較: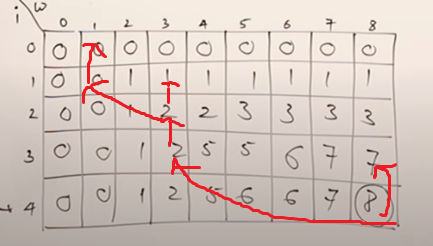
,因為每一個物品 都是 跟 上一個物品 在比較 要不要放進袋子 。
所以可以只 存 上一個物品的 價值 ,也就是只需要一維陣列。
所以 背包問題 優化後的 時間複雜度是: 物品個數 * 背包總重量
空間複雜度是 : 背包總重量
接著來看 Fractional Knapsack Problem 。
跟01問題不同的地方,就是物品可以是分數 。
Fractional Knapsack Problem | GeeksforGeeks
https://www.youtube.com/watch?v=m1p-eWxrt6g&ab_channel=GeeksforGeeks
Fractional Knapsack Problem
https://www.geeksforgeeks.org/fractional-knapsack-problem/
每一個物品 ,都先 價值 / 重量 。
就變成 1 單位的重量 ,價值多少 。
就 從 1 單位的重量 ,價值 最高的開始放到背包 。 如果那個物品的重量 大於 背包剩餘重量 。
那 就 只放 背包剩餘重量 的重量 。
像是 這個物品 重量30公斤 ,背包只剩下20公斤的重量 。
那 這個物品 可以只放20公斤 , 然後價值 就是原本的 2/3 倍 。
這個演算法的時間複雜度是 O(nlogn)
nlogn應該是指 把 每一個物品的 1單位重量的價值 排序的時間
